Favicon

Affine transformation

Peponi │ 3/28/2025 │ 11m

C#
NugetPackageOpenCvSharp4TranslateRotateReflectScaleShearMatrix

1. Introduction

OpenCV의 아핀 변환은 2D 공간에서 행렬을 변환하는 데 사용되는 3 point 선형 변환이다. 선과 평행도는 유지하며 선 사이의 각도 또는 점 사이의 거리는 달라질 수도 있다. 아핀 변환을 수학적으로 표현하면 다음과 같다.

  1. Transformation matrix
    아핀 변환을 위한 변환 행렬은 2∗32 * 3 행렬로 표현된다. Matt=[l00l01txl10l11ty]Wherelij=Linear  transformationti=Translation\begin{align} &Mat_t = \begin{bmatrix} l_{00} & l_{01} & t_x \\ l_{10} & l_{11} & t_y \notag \end{bmatrix}\\ &Where \quad \begin{align} &l_{ij} = Linear \,\, transformation \notag \\ & t_{i} = Translation \notag \end{align} \end{align}
  2. Homogeneous coordinates
    2차원 좌표 [xy]\begin{bmatrix} x \\ y \end{bmatrix}를 변환하기 위해 동차 좌표인 [xy1]\begin{bmatrix} x \\ y \\ 1 \end{bmatrix}로 표현한다. Imageo=[xy1]Image_o = \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}
  3. Computation
    MattMat_t와 ImageoImage_o를 곱하여 ImagetImage_t [x′y′]\begin{bmatrix} x' \\ y' \end{bmatrix} 를 산출한다. Imaget=Matt⋅Imageo=[l00l01txl10l11ty]⋅[xy1]=[l00x+l01y+txl10x+l11y+ty]\begin{align} Image_t &= Mat_t \cdot Image_o \notag\\ &= \begin{bmatrix} l_{00} & l_{01} & t_x \\ l_{10} & l_{11} & t_y \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \notag\\ &= \begin{bmatrix} l_{00}x+l_{01}y+t_x \\ l_{10}x+l_{11}y+t_y \end{bmatrix} \notag \end{align}

OpenCV에서는 transformation matrix를 이용한 변환과 point to point 변환을 지원한다. 이 문서에서는 MattMat_t를 이용한 연산 예시 및 point to point 변환을 소개한다.

실습에 사용할 이미지는 다음과 같다.

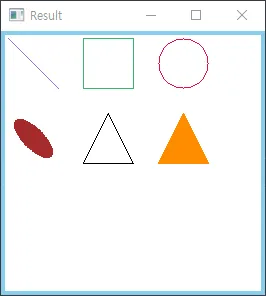
sampleImage

2. Translation

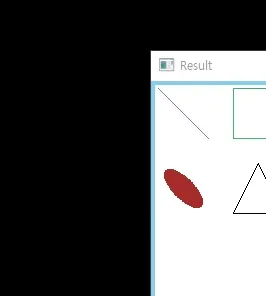
translation

Translation을 수행하면 이미지의 X, Y축 위치를 변경할 수 있다. 이 때 수행되는 연산은 다음과 같다.

Matt=[10tx01ty]Mat_t = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \end{bmatrix} Imageo=[xy1]Image_o = \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} Imaget=Matt⋅Imageo=[10tx01ty]⋅[xy1]=[x+txy+ty]\begin{align} Image_t &= Mat_t \cdot Image_o \notag\\ &= \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \notag\\ &= \begin{bmatrix} x+t_x \\ y+t_y \end{bmatrix} \notag \end{align} 
private void Translate(Mat image)
{
    // 단위행렬 생성 (1행 : [1, 0, 0],  2행 : [0, 1, 0])
    using Mat translation = Mat.Eye(2, 3, MatType.CV_32F);
 
    // Set(row, col, value)
    translation.Set<float>(0, 2, 150);  // 1행 : [1, 0, 150]
    translation.Set<float>(1, 2, 50);   // 2행 : [0, 1, 50]
 
    // Translate
    using var translated = new Mat();
    Cv2.WarpAffine(image, translated, translation, new OpenCvSharp.Size(image.Width, image.Height));
}

3. Rotation

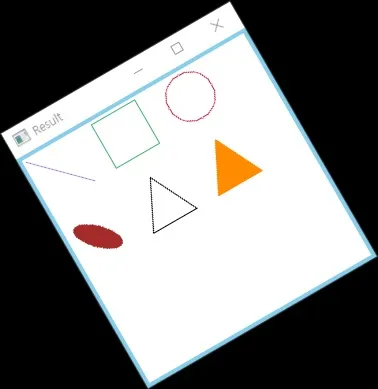
rotation

Rotation을 수행하면 이미지를 원하는 각도만큼 회전시킬 수 있다. 이 때 수행되는 연산은 다음과 같다.

Matt=[cosθ−sinθtxsinθcosθty]Mat_t = \begin{bmatrix} cos\theta & -sin\theta & t_x \\ sin\theta & cos\theta & t_y \end{bmatrix} Imageo=[xy1]Image_o = \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} Imaget=Matt⋅Imageo=[cosθ−sinθtxsinθcosθty]⋅[xy1]=[x⋅cosθ−y⋅sinθ+txx⋅sinθ+y⋅cosθ+ty]\begin{align} Image_t &= Mat_t \cdot Image_o \notag \\ &= \begin{bmatrix} cos\theta & -sin\theta & t_x \\ sin\theta & cos\theta & t_y \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \notag \\ &= \begin{bmatrix} x \cdot cos\theta - y \cdot sin\theta + t_x \\ x \cdot sin\theta + y \cdot cos\theta + t_y \end{bmatrix} \notag \end{align} 
private void Rotate(Mat image, double angle)
{
    // 빈 행렬 생성 (1행 : [0, 0, 0],  2행 : [0, 0, 0])
    using Mat rotation = Mat.Zeros(new OpenCvSharp.Size(3, 2), MatType.CV_32F);
 
    (OpenCvSharp.Size size, float tx, float ty) = ComputeSizeAndTranslation(image.Width, image.Height, angle);
 
    // Set(row, col, value)
    rotation.Set(0, 0, (float)Math.Cos(angle));       // 1행 : [cos(angle), 0, 0]
    rotation.Set(0, 1, -1 * (float)Math.Sin(angle));  // 1행 : [cos(angle), -sin(angle), 0]
    rotation.Set(0, 2, tx);                                    // 1행 : [cos(angle), -sin(angle), tx]
    rotation.Set(1, 0, (float)Math.Sin(angle));       // 2행 : [sin(angle, 0, 0]
    rotation.Set(1, 1, (float)Math.Cos(angle));      // 2행 : [sin(angle, cos(angle), 0]
    rotation.Set(1, 2, ty);                                   // 2행 : [sin(angle, cos(angle), ty]
 
    // Rotate
    using var rotated = new Mat();
    Cv2.WarpAffine(image, rotated, rotation, size);
 
    (OpenCvSharp.Size Size, float Tx, float Ty) ComputeSizeAndTranslation(int width, int height, double angle)
    {
        double tx = 0, ty = 0;
 
        // 각도 양수로 변경
        angle = angle >= 0 ? angle : Math.PI * 2 + angle;
 
        // Get quadrant constants
        (int sin, int cos) = angle switch
        {
            > Math.PI * 1.5 and <= Math.PI * 2 => (-1, 1),
            > Math.PI and <= Math.PI * 1.5 => (-1, -1),
            > Math.PI / 2 and <= Math.PI => (1, -1),
            _ => (1, 1)
        };
 
        // 최종 이미지 size 산출
        OpenCvSharp.Size size = new()
        {
            Width = (int)(cos * width * Math.Cos(angle) + sin * height * Math.Sin(angle)),
            Height = (int)(sin * width * Math.Sin(angle) + cos * height * Math.Cos(angle))
        };
 
        // ROI 바깥에 그려지는 영역 끌어오기 위한 tx, ty 계산
        switch (angle)
        {
            case > Math.PI * 1.5 and <= Math.PI * 2:
                ty = -width * Math.Sin(angle);
                break;
 
            case > Math.PI and <= Math.PI * 1.5:
                tx = -width * Math.Cos(angle);
                ty = size.Height;
                break;
 
            case > Math.PI / 2 and <= Math.PI:
                tx = size.Width;
                ty = -height * Math.Cos(angle);
                break;
 
            default:
                tx = height * Math.Sin(angle);
                break;
        }
 
        return (size, (float)tx, (float)ty);
    }
}

TIP

Cv2.Rotate(), Cv2.GetRotationMatrix2D()를 이용하여 rotation을 쉽게 수행할 수 있다.
자세한 내용은 Translate, rotate image를 참조한다.

4. Reflection

x reflectionX reflection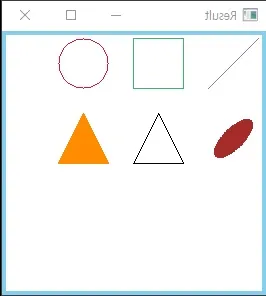
y reflectionY reflection
xy reflection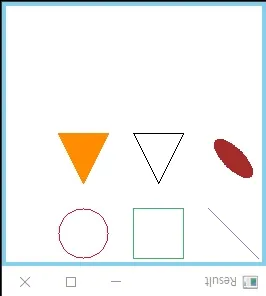XY reflection

Reflection을 수행하면 이미지를 특정 축을 중심으로 뒤집을 수 있다. 이 때 수행되는 연산은 다음과 같다.

Mattx=[10tx0−1ty]Mat_{tx} = \begin{bmatrix} 1 & 0 & t_x \\ 0 & -1 & t_y \end{bmatrix} Matty=[−10tx01ty]Mat_{ty} = \begin{bmatrix} -1 & 0 & t_x \\ 0 & 1 & t_y \end{bmatrix} Mattxy=[−10tx0−1ty]Mat_{txy} = \begin{bmatrix} -1 & 0 & t_x \\ 0 & -1 & t_y \end{bmatrix} Imageo=[xy1]Image_o = \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} Imaget=Matt⋅Imageo=[ry0tx0rxty]⋅[xy1]=[ryx+txrxy+ty]\begin{align} Image_t &= Mat_t \cdot Image_o \notag\\ &= \begin{bmatrix} r_y & 0 & t_x \\ 0 & r_x & t_y \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \notag\\ &= \begin{bmatrix} r_yx+t_x \\ r_xy+t_y \end{bmatrix} \notag \end{align} 
private void ReflectX(Mat image)
{
    // 빈 행렬 생성 (1행 : [0, 0, 0],  2행 : [0, 0, 0])
    using Mat reflection = Mat.Zeros(new OpenCvSharp.Size(3, 2), MatType.CV_32F);
 
    // Set(row, col, value)
    reflection.Set<float>(0, 0, 1);   // 1행 : [1, 0, 0]
    reflection.Set<float>(1, 1, -1);  // 2행 : [0, -1, 0]
    reflection.Set<float>(1, 2, image.Height);  // 2행 : [0, -1, image.Height], ROI 바깥에 그려지는 영역 끌어옴
 
    // Reflect
    using var reflected = new Mat();
    Cv2.WarpAffine(image, reflected, reflection, new OpenCvSharp.Size(image.Width, image.Height));
}
private void ReflectY(Mat image)
{
    // 빈 행렬 생성 (1행 : [0, 0, 0],  2행 : [0, 0, 0])
    using Mat reflection = Mat.Zeros(new OpenCvSharp.Size(3, 2), MatType.CV_32F);
 
    // Set(row, col, value)
    reflection.Set<float>(0, 0, -1);                  // 1행 : [-1, 0, 0]
    reflection.Set<float>(0, 2, image.Width);  // 1행 : [-1, 0, image.Width], ROI 바깥에 그려지는 영역 끌어옴
    reflection.Set<float>(1, 1, 1);                    // 2행 : [0, 1, 0]
 
    // Reflect
    using var reflected = new Mat();
    Cv2.WarpAffine(image, reflected, reflection, new OpenCvSharp.Size(image.Width, image.Height));
}
private void ReflectXY(Mat image)
{
    // 빈 행렬 생성 (1행 : [0, 0, 0],  2행 : [0, 0, 0])
    using Mat reflection = Mat.Zeros(new OpenCvSharp.Size(3, 2), MatType.CV_32F);
 
    // Set(row, col, value)
    reflection.Set<float>(0, 0, -1);                   // 1행 : [-1, 0, 0]
    reflection.Set<float>(0, 2, image.Width);   // 1행 : [-1, 0, image.Width], ROI 바깥에 그려지는 영역 끌어옴
    reflection.Set<float>(1, 1, -1);                   // 2행 : [0, -1, 0]
    reflection.Set<float>(1, 2, image.Height);  // 2행 : [0, -1, image.Height], ROI 바깥에 그려지는 영역 끌어옴
 
    // Reflect
    using var reflected = new Mat();
    Cv2.WarpAffine(image, reflected, reflection, new OpenCvSharp.Size(image.Width, image.Height));
}

TIP

Mat.Flip()을 이용하여 reflection을 쉽게 수행할 수 있다.
자세한 내용은 Flip image를 참조한다.

5. Scaling

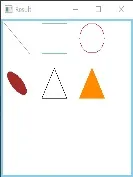
scaling

Scaling을 수행하면 이미지의 크기를 지정한 배율에 맞게 설정할 수 있다. 이 때 수행되는 연산은 다음과 같다.

Matt=[Scalex000Scaley0]Mat_{t} = \begin{bmatrix} Scale_x & 0 & 0 \\ 0 & Scale_y & 0 \end{bmatrix} Imageo=[xy1]Image_o = \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} Imaget=Matt⋅Imageo=[Scalex000Scaley0]⋅[xy1]=[x⋅Scalexy⋅Scaley]\begin{align} Image_t &= Mat_t \cdot Image_o \notag\\ &= \begin{bmatrix} Scale_x & 0 & 0 \\ 0 & Scale_y & 0 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \notag\\ &= \begin{bmatrix} x \cdot Scale_x \\ y \cdot Scale_y \end{bmatrix} \notag \end{align} 
private void Scale(Mat image, float scaleX, float scaleY)
{
    // 빈 행렬 생성 (1행 : [0, 0, 0],  2행 : [0, 0, 0])
    using Mat scale = Mat.Zeros(new OpenCvSharp.Size(3, 2), MatType.CV_32F);
 
    // Set(row, col, value)
    scale.Set(0, 0, scaleX);    // 1행 : [scaleX, 0, 0]
    scale.Set(1, 1, scaleY);    // 2행 : [0, scaleY, 0]
 
    // Scale
    using var scaled = new Mat();
    Cv2.WarpAffine(image, scaled, scale, new OpenCvSharp.Size(image.Width * scaleX, image.Height * scaleY));
}

TIP

Mat.Resize()을 이용하여 scaling을 쉽게 수행할 수 있다.
자세한 내용은 Resize image를 참조한다.

6. Shearing

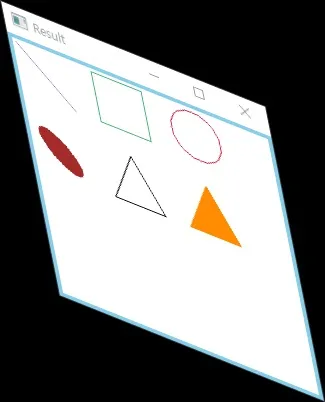
shearing

Shearing을 수행하면 이미지를 기울일 수 있다. 이 때 수행되는 연산은 다음과 같다.

Matt=[1ShearxtxSheary1ty]Mat_{t} = \begin{bmatrix} 1 & Shear_x & t_x \\ Shear_y & 1 & t_y \end{bmatrix} Imageo=[xy1]Image_o = \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} Imaget=Matt⋅Imageo=[1ShearxtxSheary1ty]⋅[xy1]=[x+y⋅Shearx+txx⋅Sheary+y+ty]\begin{align} Image_t &= Mat_t \cdot Image_o \notag\\ &= \begin{bmatrix} 1 & Shear_x & t_x \\ Shear_y & 1 & t_y \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \notag\\ &= \begin{bmatrix} x + y \cdot Shear_x + t_x \\ x \cdot Shear_y + y + t_y \end{bmatrix} \notag \end{align} 
private void Shear(Mat image, float shearX, float shearY)
{
    // 단위행렬 생성 (1행 : [1, 0, 0],  2행 : [0, 1, 0])
    using Mat shear = Mat.Eye(2, 3, MatType.CV_32F);
 
    // Set(row, col, value)
    shear.Set(0, 1, shearX);    // 1행 : [1, shearX, 0]
    if (shearX < 0)
    {
        shear.Set(0, 2, image.Height * Math.Abs(shearX));    // 1행 : [1, shearX, image.Height * Math.Abs(shearX)], ROI 바깥에 그려지는 영역 끌어옴
    }
    shear.Set(1, 0, shearY);    // 2행 : [shearY, 1, 0]
    if (shearY < 0)
    {
        shear.Set(1, 2, image.Width * Math.Abs(shearY));   // 2행 : [shearY, 1, image.Width * Math.Abs(shearY)], ROI 바깥에 그려지는 영역 끌어옴
    }
 
    var width = image.Width + (image.Height * Math.Abs(shearX));
    var height = image.Height + (image.Width * Math.Abs(shearY));
 
    // Shear
    using var sheared = new Mat();
    Cv2.WarpAffine(image, sheared, shear, new OpenCvSharp.Size(width, height));
}

7. Point to point 변환

point to point

연산을 수행할 3개의 좌표와 이동 좌표를 알고 있다면 Cv2.GetAffineTransform()를 통해 transformation matrix를 얻은 후 아핀 변환을 수행할 수 있다.

private void PointToPoint(Mat image)
{
    // 각 collection의 순서에 맞춰 변환
    List<Point2f> origin = [
        new(50,50),
        new(150,50),
        new(50,200)
        ];
    List<Point2f> destination = [
        new(150,150),
        new(200,200),
        new(100,250)
        ];
 
    // 이미지에 초기 좌표 표시
    origin.ForEach(point => Cv2.Circle(image, new(point.X, point.Y), 5, Scalar.Crimson, -1));
 
    // 아핀 맵 행렬 생성
    using var affine = Cv2.GetAffineTransform(origin, destination);
 
    // Transform
    using var affineTransformed = new Mat();
    Cv2.WarpAffine(image, affineTransformed, affine, new OpenCvSharp.Size(image.Width, image.Height));
}

8. 참조 자료